<문제>

<문제 풀이>
이분 탐색이라고 해서 나무 자르기 같은 문제인지 알았는데 그건 또 아니었다.
아예 다른 유형의 문제였는데 LIS(Longest Increasing Subseqence)가 가장 긴 증가하는 부분 수열을 찾는 문제라고 한다.
자 그래서 어떻게 찾냐 찾는 방법이 3가지 있는데
1. dp[x] 동적으로 찾는 법
2. 세그먼트 트리로 찾는 법
3. 이분탐색으로 찾는 법
3가지가 있다.
그 중 이분탐색으로 찾는 법을 알아볼건데 이게 기존에 있던 배열을 가지고 새로운 배열을 만들면서 시작된다.
1. 기존 배열 (=list)의 첫 원소를 새로운 배열(vector)에 입력한다.
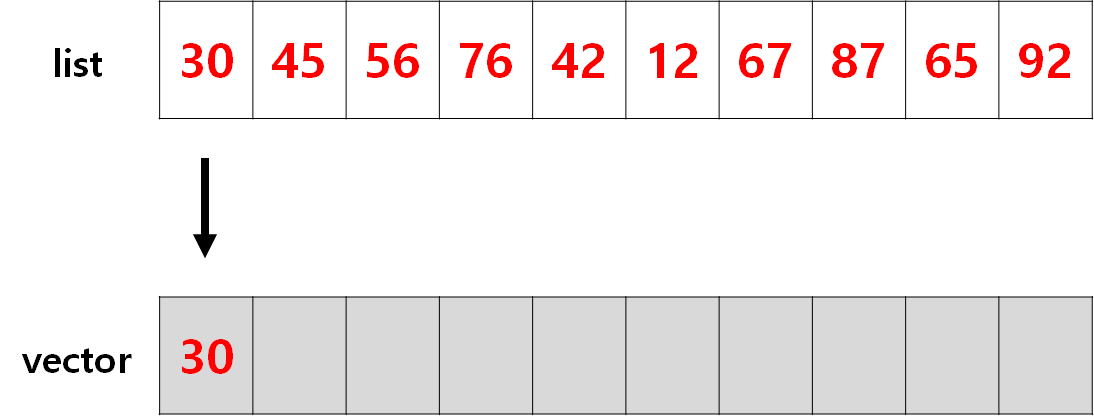
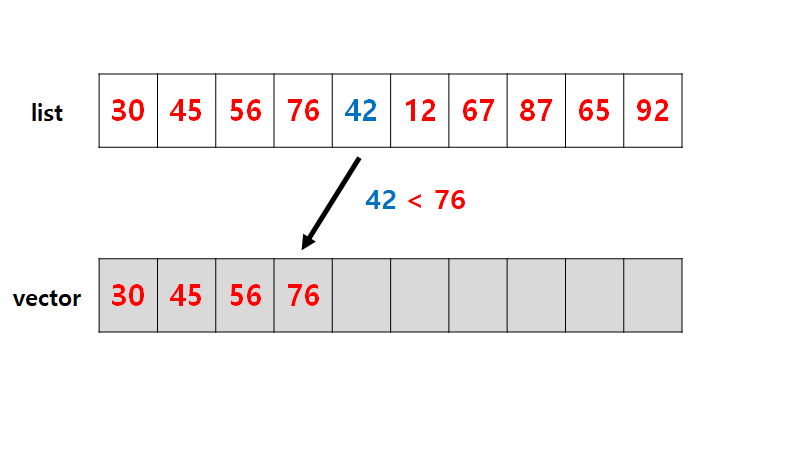
2. 이 후, vector의 마지막 원소=v_elem와 list의 원소(idx=1 부터 끝까지)=l_elem를 비교한다. 비교 시, v_elem이 l_elem보다 작다면 (v_elem < l_elem) 계속해서 vector에 l_elem을 추가 시킨다.

3.만약 v_elem이 l_elem보다 크거나 같다면 (v_elem >= l_elem) vector에서 이분탐색을 통해(lower_bound) vecotr내에서 l_elem보다 크거나 같은 값 중 최솟값을 찾은 다음 해당 값을 l_elem으로 교체한다.

4. 위 과정을 반복하면 LIS가 산출 된다. (단, vector에 있는 원소가 실제 LIS의 원소와 같진 않다. 단지 vector는 가장 긴 부분 수열의 값을 찾아낼 뿐이다.)

5. 정당성 난 그런거 잘모르겠고 문제 유형을 보고 외우고 응용하고 배운다. 앞으로 이런문제가 나오면 까먹지말고 잘하자.
<코드 구현>
#include <iostream>
#include <algorithm>
#include <vector>
#define MAX 1000001
using namespace std;
vector<int> list;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N;
int idx;
vector<int> answer;
cin >> N;
list = vector<int>(N, 0);
for (int i = 0; i < N; ++i) {
cin >> list[i];
}
answer.push_back(list[0]);
for (int i = 1; i < list.size(); ++i) {
if (answer[answer.size() - 1] >= list[i]) {
idx = lower_bound(answer.begin(), answer.end(), list[i]) - answer.begin();
answer[idx] = list[i];
}
else answer.push_back(list[i]);
}
cout << answer.size() << '\n';
}
'백준 문제 풀이' 카테고리의 다른 글
| [DFS/BFS] 9202번 Boggle (0) | 2021.04.20 |
|---|---|
| [DFS/BFS] 15559번 내 선물을 받아줘 (0) | 2021.04.19 |
| [이분 탐색] 2805번 나무 자르기 (0) | 2021.03.05 |
| [다익스트라] 1573번 최단경로 (0) | 2021.02.22 |
| [모스(Mo's) 알고리즘] 13547번 수열과 쿼리 5 (0) | 2021.02.17 |